PUBLICIDAD
Si te gusta esta web (que no es todavía la mejor, pero trabajo duro para que lo sea), por favor, pulsa el botón 'Me gusta'. ¡Muchas gracias!
(Para cumplir con la normativa comunitaria, los botones no aparecerán si no estás conectado, en otra ventana, a tu cuenta en Facebook)
Muy importante: No pulsar el botón 'Me gusta' si ya se ha pulsado anteriormente (aunque haya sido hace tiempo), pues disminuiria el contador.
Si al pulsar disminuye, es porque ya habías pulsado antes, entonces vuelve a pulsar y aumentará.
| ¿Quieres recibir en tu correo electrónico, diariamente y de forma gratuita, chistes, memes, así como temas graciosos, curiosos y de interés general? Pulsa el botón → Suscribirse a los boletines de LuisSkier |
PUBLICIDAD
¿Qué es un objeto imposible? Pues es aquel que podemos dibujar, pero que si intentamos construirlo de forma que lo podamos tocar, ¡narices! ¡no hay forma!, es decir, son posibles en dos dimensiones, pero, no son posibles en el plano tridimensional, o hablando más académicamente: se conocen como objetos imposibles a aquellos que su construcción en las tres dimensiones conocidas (ancho, largo y profundidad o altura) no se puede dar (aunque si es posible la representación bidimensional de estos objetos por medio de dibujos u otros recursos tecnológicos).
(NOTA.- Pulsa sobre cualquier imagen para verla a mayor tamaño y con su pie de foto correspondiente.)
De estos objetos imposibles el más conocido es sin duda el 'Triángulo de Penrose' (que se puede ver en la imagen superior). Este objeto imposible, que fue definido por Penrose como la 'imposibilidad en su forma más pura', ha dado origen a distintos logotipos entre ellos, uno conocido por todos, el logotipo del reciclaje.
En muchas ciudades del mundo hay instaladas esculturas que observadas desde el punto adecuado permiten la ilusión óptica del 'Triángulo de Penrose'. De ellas, la instalada en la ciudad de Perth (Australia) con sus 13,5 metros de altura es la de mayores dimensiones (ver figura).
Si te gusta esta web (que no es todavía la mejor, pero trabajo duro para que lo sea), por favor, pulsa el botón 'Me gusta'. ¡Muchas gracias!
(Para cumplir con la normativa comunitaria, los botones no aparecerán si no estás conectado, en otra ventana, a tu cuenta en Facebook)
Muy importante: No pulsar el botón 'Me gusta' si ya se ha pulsado anteriormente (aunque haya sido hace tiempo), pues disminuiria el contador.
Si al pulsar disminuye, es porque ya habías pulsado antes, entonces vuelve a pulsar y aumentará.
Otros polígonos de Penrose.-
Es posible construir en base a un triángulo de Penrose, otros polígonos regulares, creando así un polígono de Penrose, aunque el efecto visual no es tan impactante, ya que al incrementarse el número de lados, la imagen parece distorsionada o retorcida. Asimismo existe una escalera imposible, la 'Escalera de Penrose' y la versión de Ernst.
PUBLICIDAD
En el siguiente vídeo se explica como dibujar un triángulo de Penrose.
Si te gusta esta web (que no es todavía la mejor, pero trabajo duro para que lo sea), por favor, pulsa el botón 'Me gusta'. ¡Muchas gracias!
(Para cumplir con la normativa comunitaria, los botones no aparecerán si no estás conectado, en otra ventana, a tu cuenta en Facebook)
Muy importante: No pulsar el botón 'Me gusta' si ya se ha pulsado anteriormente (aunque haya sido hace tiempo), pues disminuiria el contador.
Si al pulsar disminuye, es porque ya habías pulsado antes, entonces vuelve a pulsar y aumentará.
El siguiente vídeo muestra la ilusión óptica del triangulo de Penrose en uno instalado en una calle de Ophoven (Bélgica). Utiliza una técnica ligeramente distinta pero igual de efectiva al instalado en la ciudad de Perth (Australia).
PUBLICIDAD
Otras ilusiones ópticas.-
La Escalera de Penrose (o Escalera Infinita).-
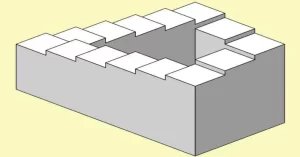
Otra ilusión óptica u objeto imposible es la 'Escalera de Penrose', escalera que es la representación bidimensional de unas escaleras que cambian su dirección 90 grados cuatro veces mientras da la sensación de que suben o bajan a la vez, sea la dirección que sea.
El ejemplo más conocido de la escalera de Penrose aparece en la famosa litografía 'Klimmen en Dalen' (en español 'Ascenso y Descenso') de Maurits Cornelis Escher, donde se incorpora a la torre de una fortaleza con los soldados ascendiendo o descenciendo continuamente.
Escher se basó en la Escalera de Penrose, un problema matemático que obsesionó a Escher, y en 1960 dibujó su famosa litografía (38 cm × 28,5 cm) 'Ascenso y Descenso', que representa una torre en la que un grupo de soldados o bien no paran de subir (los que van por el exterior) o no paran de bajar (los del interior) en una escalera sin fin.
Maurits Cornelis Escher (Leeuwarden, 17 de junio de 1898-Hilversum, 27 de marzo de 1972) fue un artista neerlandés conocido por sus dibujos que consisten en figuras imposibles, teselados y mundos imaginarios.
Otra de sus obras famosa es 'Otro Mundo' (1947). En ella podemos ver un edificio de ladrillo desde tres perspectivas diferentes con un paisaje astronómico al fondo. En el centro y a la izquierda se ve un paisaje lunar a través de unos arcos. En el cielo se puede ver un cometa, el planeta Júpiter con los cuatro satélites descubiertos por Galileo, un cúmulo globular y otros objetos astronómicos.
El paisaje cubierto de cráteres ofrece una imagen de nuestro satélite típicamente anterior a la llegada del hombre a la Luna.
Si te gusta esta web (que no es todavía la mejor, pero trabajo duro para que lo sea), por favor, pulsa el botón 'Me gusta'. ¡Muchas gracias!
(Para cumplir con la normativa comunitaria, los botones no aparecerán si no estás conectado, en otra ventana, a tu cuenta en Facebook)
Muy importante: No pulsar el botón 'Me gusta' si ya se ha pulsado anteriormente (aunque haya sido hace tiempo), pues disminuiria el contador.
Si al pulsar disminuye, es porque ya habías pulsado antes, entonces vuelve a pulsar y aumentará.
En el siguiente vídeo ........... FALTA TEXTO .......
PUBLICIDAD
La Escalera de Penrose (versión de Ernst)
FALTA EL TEXTO
La Cascada de Escher.-
La Cascada de M.C. Escher representa una corriente de agua que fluye en zigzag a lo largo de los lados de dos triángulos de Penrose alargados, de tal forma que acaba dos pisos más arriba de donde comienza. La catarata resultante, formada en los lados cortos de ambos triángulos, hace funcionar una noria. Escher puntualiza que para poder mantener la noria funcionando, es necesario agregar de vez en cuando algo de agua, para compensar las pérdidas por evaporación.
Ilusiones ópticas.-
Las ilusiones ópticas son imágenes capaces de alterar nuestro mecanismo de visión de manera que provocan que percibamos la realidad de forma distinta o ambigua, ya que nuestro cerebro no es capaz de interpretarla de una manera lógica. Existen dos tipos:
- Las ilusiones ópticas de tipo fisiológico que son aquellas asociadas a los efectos de una estimulación excesiva en los ojos o el cerebro (brillo, color, movimiento, etc., como el encandilamiento tras ver una luz potente).
- Las ilusiones ópticas cognitivas en las que se muestra algún tipo de ambigüedad o distorsión que nos impide interpretar correctamente la imagen
Si te gusta esta web (que no es todavía la mejor, pero trabajo duro para que lo sea), por favor, pulsa el botón 'Me gusta'. ¡Muchas gracias!
(Para cumplir con la normativa comunitaria, los botones no aparecerán si no estás conectado, en otra ventana, a tu cuenta en Facebook)
Muy importante: No pulsar el botón 'Me gusta' si ya se ha pulsado anteriormente (aunque haya sido hace tiempo), pues disminuiria el contador.
Si al pulsar disminuye, es porque ya habías pulsado antes, entonces vuelve a pulsar y aumentará.
Debajo existe una galería de imágenes que ocultan o enmascaran otros objetos o que provocan distintos efectos o engaños a nuestra mente y que por lo tanto, no somos capaces de interpretarlas correctamente o lo hacemos de forma incompleta.
Usa las flechas de navegación situadas debajo para desplazarte a la imagen anterior o siguiente.
Arriba o abajo
PUBLICIDAD
| ← Tema anterior | Tema siguiente → | |
| ¿Quieres recibir en tu correo electrónico, diariamente y de forma gratuita, chistes, memes, así como temas graciosos, curiosos y de interés general? Pulsa el botón → Suscribirse a los boletines de LuisSkier |
| 1er. 'Sabias qué ... ' | Menú 'Sabias qué ... ' |
| El Humor del Día | El Tema de la Semana | ||
| Todos los Chistes | Chistes cortos | ||
| Historietas graciosas | Historias curiosas |
